본 포스팅은 “케라스 창시자에게 배우는 딥러닝” - (길벗출판사, 프랑소와 숄레 지음, 박해선 옮김)을 바탕으로 공부한 내용을 정리한 것입니다.
- 신경망 구조
- 활성화 함수
- Sigmoid 함수
- Tanh 함수
- ReLU (Rectified Linear Unit) 함수
- Leaky ReLU
- PReLU
- ELU (Exponential Linear Unit)
- Maxout
이전 포스팅과 함께 보자.
1. 신경망 구조
1
2
3
4
5
6
from tensorflow.keras import models
from tensorflow.keras import layers
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))
신경망의 핵심 구성 요소는 층 (layer)다.
여과기 같은 일종의 데이터 처리 필터라고도 생각 할 수 있다.
완전 연결 (fully connected)된 신경망 층인 Dense 층 2개가 연속되어 있다.
마지막 층은 소프트맥스 (softmax) 층이다.
2. 활성화 함수
첫 번째 층의 활성화 함수로 relu 함수가 사용되었다.
비선형 함수를 사용하여 딥러닝 모델의 레이어를 깊게 가져갈 수 있다고 한다.
대표적으로 사용되는 활성화 함수는 다음과 같다. (미분 결과는 생략한다)
Sigmoid 함수
\[sigmoid(x) = \frac{1}{1+e^{-x}}\]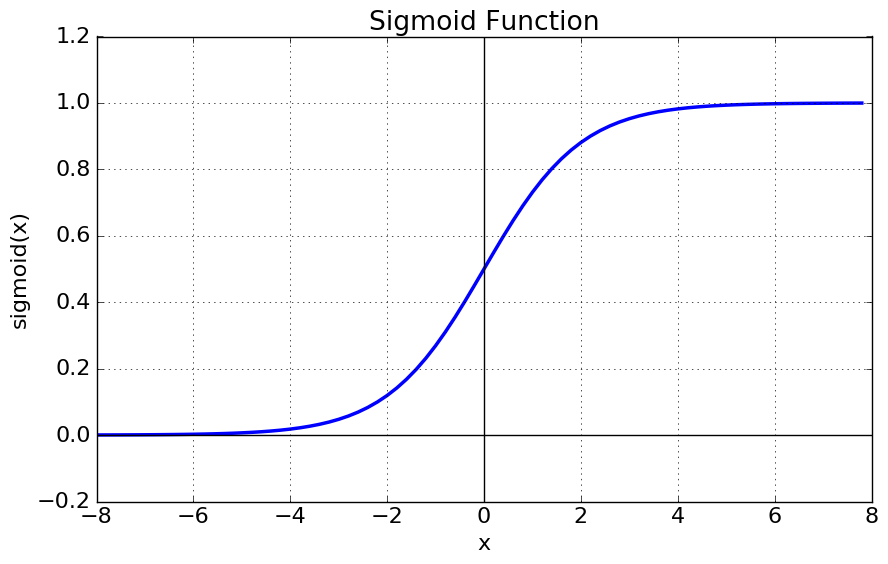
Logistic 함수라고 불리기도 한다. $x$의 값에 따라 0 ~ 1의 값을 출력한다.
Gradient Vanishing 현상, 함수값 중심이 0 이 아닌 $1 \over 2$, $\exp$ 함수 사용 등의 단점
Tanh 함수
\[tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\] \[tanh(x) = 2 \sigma (2x) - 1\]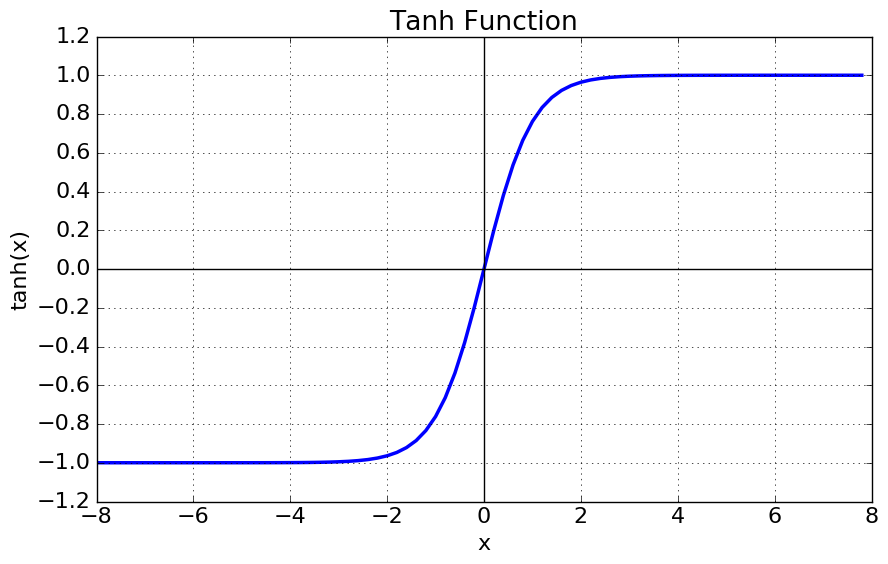
$\sigma$는 sigmoid 함수이다.중심값이 0이 되어 sigmoid의 최적화 과정이 느려지는 문제는 해결.
여전히 남아있는 Gradient Vanishing의 단점
ReLU (Rectified Linear Unit) 함수
\[f(x) = max(0,x)\]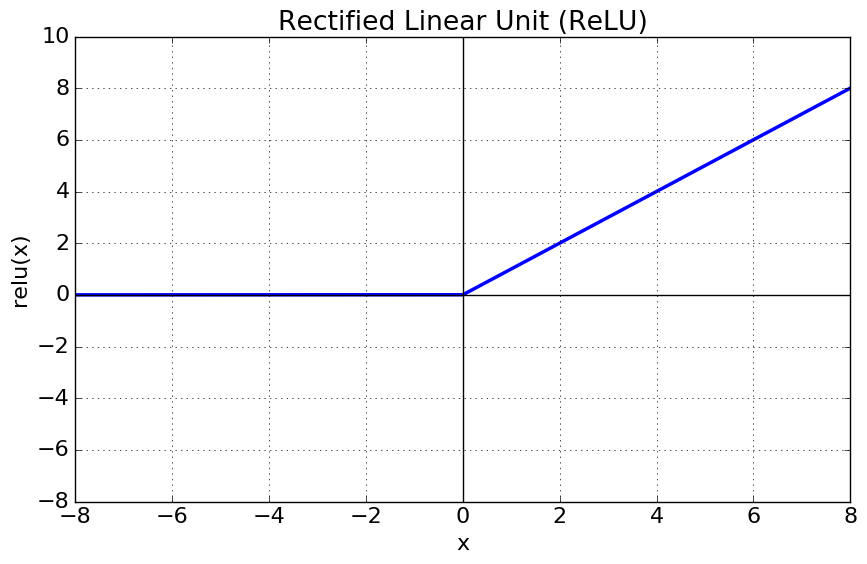
sigmoid, tanh 보다 빠른학습, $x < 0$에서 뉴런이 죽을 수 있는 단점
Leaky ReLU
\[f(x) = max(0.01x,x)\]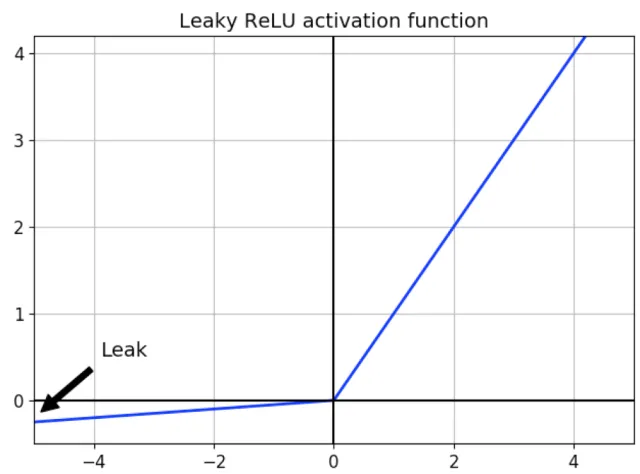
ReLU 함수의 뉴런이 죽는 현상 (Dying ReLU)을 해결하기 위해 등장. 0.01 대신 다른 매우 작은 값을 사용 가능
PReLU
\[f(x) = max(\alpha x,x)\]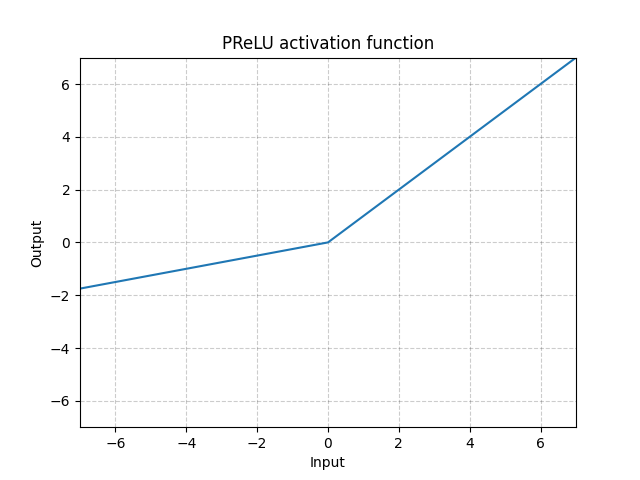
Leaky ReLU와 유사하지만 $\alpha$로 $x < 0$에서 기울기를 학습 가능
ELU (Exponential Linear Unit)
\[f(x) = \begin{cases} x \;\qquad\qquad\; x>0\\ \alpha (e^{x}-1) \quad\; x \leq 0\end{cases}\]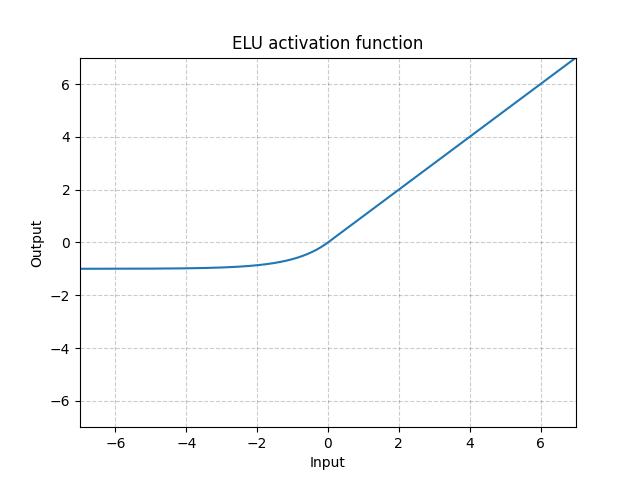
ReLU의 모든 장점을 포함, Dying ReLU 해결, 출력값의 중앙값이 0에 근사
$x \leq 0$에서 $\exp$ 함수 계산하는 비용이 발생
Maxout
\[f(x) = max(\omega_{1}^{T} x + b_{1}, \omega_{2}^{T} x + b+{2})\]여러개의 선형 함수 중 최댓값을 출력하는 함수
ReLU의 장점들과 Dying ReLU 해결. 계산량이 복잡하다는 단점
간단하고 빠른 편인 ReLU를 먼저 사용하고 Leakly ReLU, PReLU, ELU 등도 사용해본다. simoid와 tanh는 지양
deeesp 님의 포스팅 에 총 22개의 다른 활성화 함수들에 대해서도 자세히 설명이 나와있다.
참고
HDLY 님의 포스팅 딥러닝 - 활성화 함수(Activation) 종류 및 비교
reniew 님의 포스팅 딥러닝에서 사용하는 활성화함수
deeesp 님의 포스팅 [DL] Activation Functions (활성화 함수)
“케라스 창시자에게 배우는 딥러닝” - (길벗출판사, 프랑소와 숄레 지음, 박해선 옮김)
- 깃허브: http://github.com/gilbutITbook/006975
- 길벗출판사 홈페이지: http://www.gilbut.co.kr
- tensorflow 2.4 버전 코드 https://github.com/rickiepark/deep-learning-with-python-notebooks/tree/tf2
