본 포스팅은 “Do it! 강화 학습 입문” - (이지스퍼블리싱, 조규남, 맹윤호, 임지순 지음)을 바탕으로 공부한 내용을 정리한 것입니다.

강화학습
마르코프 결정 (MDP, Markov Decision Process)
- 영화를 예시로 바라보는 마르코프 결정
- 상태, 행동, 보상
- 행동에 의한 상태 전이에 확률 도입
벨만 방정식 (Bellman Equation)
- 보상 총합이 무한으로 발산하는 문제
- 시간에 따른 할인 개념 도입하기
- 보상 총합, 가치 함수
- 현재 상태의 가치 구하기, 벨만 방정식
정책
- 정책 반복법

1. 강화학습 (Reinforcement Learning)

머신러닝 (Machine Learning)은 크게 다음과 같이 나눌 수 있다.

지도학습 (Supervised Learning)
- 데이터와 레이블이 주어진 상태에서, 새 데이터에 레이블을 매기는 방법을 학습.
비지도학습 (Un-Supervised Learning)
- 레이블 없이 데이터만 주어진 상태에서, 새 데이터의 분류, 밀도 추정 등의 방법을 학습.
- 특징을 요약할 때 등.
강화학습 (Reinforcement Learning)
- 행동과 보상으로, 어떤 상태에서 최적의 행동을 찾아가는 방법을 학습.

1906년 마르코프 결정 과정(MDP, Markov Decision Process), 1950년 동적 계획법 (DP, Dynamic Programming)의 오랜 역사 이후, 강화학습은 딥러닝과의 결합 (대표적으로 DQN, Deep Q-Network)으로 다시 주목 받고 있다.

강화학습의 공부 방향

강화학습의 기본인 MDP의 용어들과 그 의미, 모델 기반 강화 학습, 모델 프리 강화 학습, 시간차 학습, Q 학습.

이후 CNN (Convolution Neural Network)과 결합한 DQN나 PPO, GPT 등으로 공부 방향을 잡으면 될 것 같다.

내가 내린 강화 학습의 짧막한 요약은 다음과 같다.

“강화 학습은 상태에서 행동에 대한 보상을 최적화 하는 함수, 정책 (Policy)을 찾는 것.”

강화 학습은 지금 상태에서 해야 할 최적의 행동이 무엇인지 방향을 세워 나가는 과정이다.

2. 마르코프 결정 (MDP, Markov Decision Process)

마르코프 결정 과정 (MDP, Markov Decision Process)은 의사 결정을 하는데 필요한 체계로 볼 수 있다.

영화를 예시로 바라보는 마르코프 결정

책에서는 이를 설명하기 위해 예시로 영화 엣지 오브 투모로우를 들고 있다.

엣지 오브 투모로우 (Edge of Tomorrow, 2014)
주인공 빌 케이지(톰 크루즈)는 외계인이 점령한 지구를 해방하기 위한 인류 연합군에서 상륙작전에 투입되고, 우연히 외계인의 시간 리셋 능력을 얻고 죽을 때마다 작전의 전날에 부활한다. 케이지는 전투와 사망을 수백 번 반복하며, 인류의 승리를 위해 싸워나간다.

강화학습의 관점에서 해당 줄거리를 바라보았을 때, 다음 그림과 같이 나타낼 수 있다.

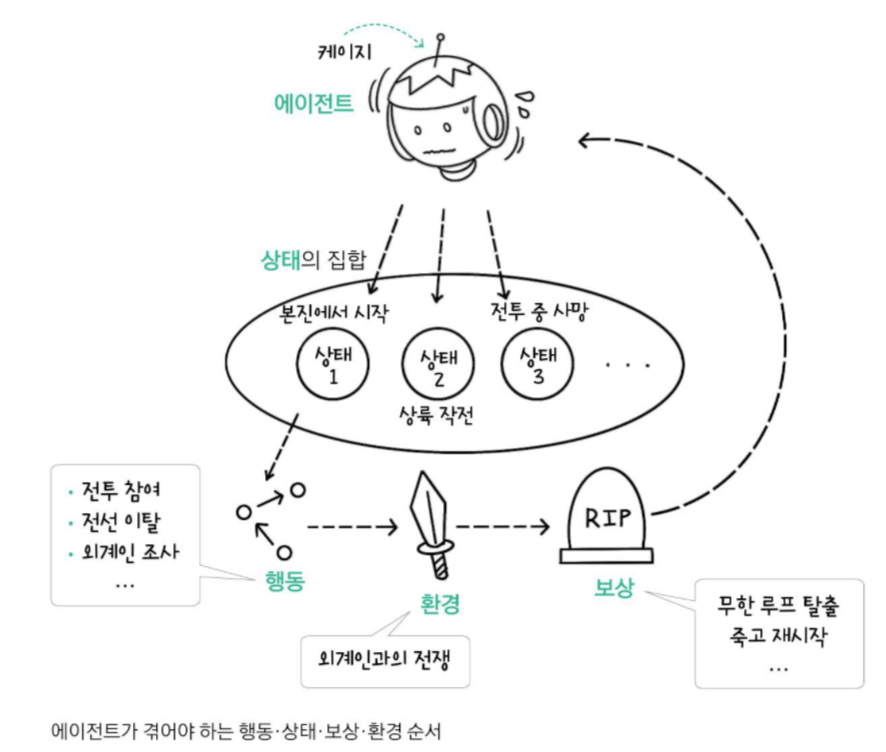
강화학습에서 에이전트 (Agent)는 해당 예시에서 행동의 주체인 주인공으로 볼 수 있다.

에이전트는 전투라는 환경에서 상호 작용하며 가장 큰 보상인 외계인 대장 제거를 위해,

죽을 때마다 작전 전날에 부활하며 초기 상태에서 출발하여,

새로운 에피소드에서 다양한 상태와 그 때의 행동을 통해 대장을 물리치는 과정을 탐색한다.

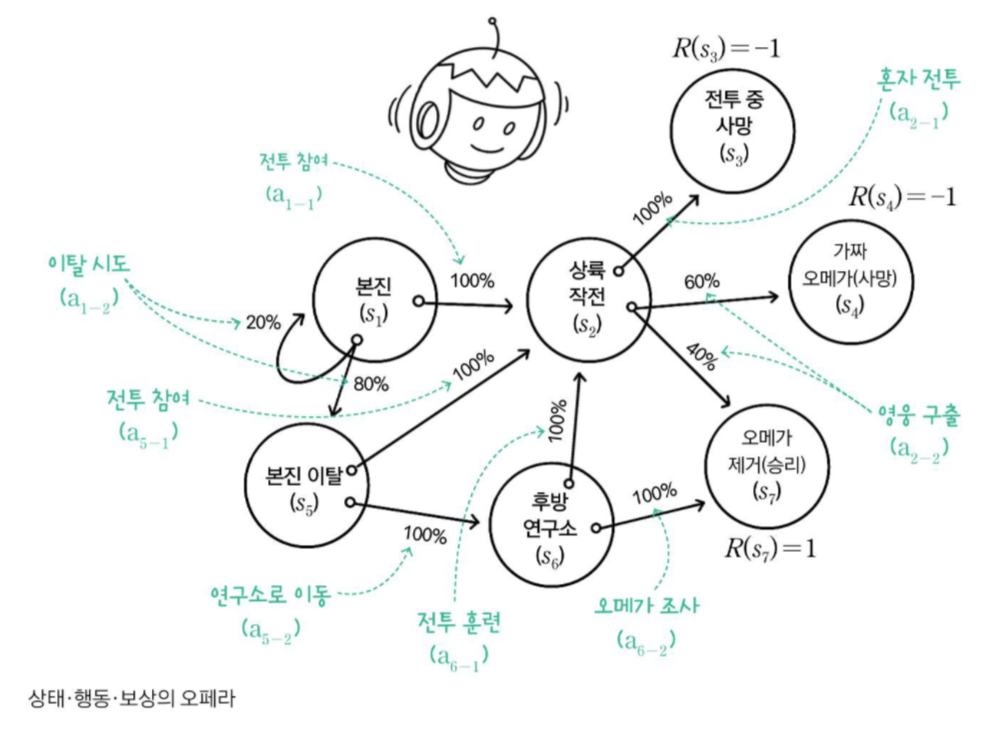
\(s_{1}\)이나 \(a_{1-1}\)과 같은 표기는 각각 상태 (state)와 행동 (action)을 의미한다.

본진(\(s_{1}\))에서 깨어난 에이전트는 상륙 작전 전투에 참가(\(a_{1-1}\)), 본진 이탈(\(a_{1-2}\))가 가능.
상륙 작전 투입(\(s_{2}\))된 에이전트는 혼자 전투(\(a_{2-1}\)), 전투를 도울 영웅을 구출(\(a_{2-2}\))가 가능.
본진 이탈(\(s_{5}\))한 에이전트는 다시 상륙 작전(\(a_{5-1}\))을 향할 수도, 비밀을 조사하러 후방 연구소로 이동(\(a_{5-2}\)) 가능.
후방 연구소 이동(\(s_{6}\))한 에이전트는 전투 훈련(\(a_{6-1}\))을 받을 수도, 외계인 보스 조사(\(a_{6-2}\))도 가능.

상태, 행동, 보상

이런 식으로 에이전트는 시작 상태와 종단 상태를 포함한 7가지 상태,

그 둘을 제외한 각 상태에서 2개의 행동을 취할 수 있다.

각 상태 \(s_{1}, s_{2}, \ldots, s_{7}\)의 상태 집합을 \(S\)로 표현하고, 행동의 집합을 \(A(s)\)로 표현.

\(s_{1}\)에서 취할 수 있는 행동의 집합은 \(A(s_{1})\)이 된다.

그림에서 각 상태에서의 보상이 명시 되어있다.

\[R(s_{3})=-1, R(s_{4})=-1, R(s_{7})=1\] \[R(s_{1})=R(s_{2})=R(s_{5})=R(s_{6})=0\]

행동에 의한 상태 전이에 확률 도입

에이전트가 \(s_{1}\)에서 \(a_{1-2}\)를 했을 때, 상태 전이에는 확률이 있다.

80% 확률로 \(s_{5}\), 20% 확률로 \(s_{1}\)로 전이될 수도 있다.

상태 전이 확률 (State Transition Probablity)는 수식으로 표현가능 하며, 상태-행동 한 쌍의 전이 확률 합은 1이다.

\[P(s_{5} \mid s_{1},a_{1-2})=0.8\] \[P(s_{1} \mid s_{1},a_{1-2})=0.2\]

이런 확률의 집합을 모델 (Model)이라 한다. 표로 이들을 표현하면 다음과 같다.

상태 (Status, S)	에이전트가 환경 내 특정 시점에서 관찰할 수 있는 것을 수치화
행동 (Action, A)	에이전트가 환경에게 전달하는 입력
보상 (Reward, R)	에이전트가 환경으로부터 전달받은 목적을 달성하기 위해 행동 수행에 대한 피드백
모델 (Model, M)	행동에 따른 상태 전이가 일어날 확률을 담은 규칙

즉, MDP는 상태 집합 \(S\)로 이루어지며, 행동 집합 \(A\)가 있고,

상태 \(s\)에서 행동 \(a\)를 통해 상태 \(s^\prime\)로 전이할 확률은 \(P(s^\prime \mid s,a)\)이며, 보상은 \(R(s,a)\)이다.

마르코프 특성 (Markov Property)를 만족한다고 가정하면 모든 상태는 직전의 상태와 행동에 의해서만 결정된다. MDP에서는 에이전트의 오직 현재 상태만 다음 상태 전이 확률에 영향을 미친다. ‘과거는 상관없다’

3. 벨만 방정식 (Bellman Equation)

장기적 보상의 예측치를 극대화하는 행동을 찾는 것. MDP 상태 안에서 최적의 행동을 찾는 방법.

에이전트가 특정 상태에서 미래 보상의 총합을 구할 수 있다고 가정하면,

보상의 예측치를 최대로 만드는 상태로 가는 행동이 곧 최적의 행동이다. 같이 식을 세워나가자.

보상 총합이 무한으로 발산하는 문제

예시로 한 에피소드에서 에이전트가 취할 수 있는 일부 상태 경로와 그에 따른 보상의 총합은 다음과 같다.

상태 경로: \(s_{1} \rightarrow s_{2} \rightarrow s_{3}\)
보상 총합: \(R(s_{1})+R(s_{2})+R(s_{3})\)
상태 경로: \(s_{1} \rightarrow s_{5} \rightarrow s_{2} \rightarrow s_{3}\)
보상 총합: \(R(s_{1})+R(s_{5})+R(s_{2})+R(s_{3})\)
상태 경로: \(s_{1} \rightarrow s_{5} \rightarrow s_{1} \rightarrow s_{5} \ldots\)
보상 총합: \(R(s_{1})+R(s_{5})+R(s_{1})+R(s_{5})+\ldots\)

이 때, 3번째 에피소드에서는 \(s_{1}\)과 \(s_{5}\)를 무한히 왕복하여, 보상 총합이 무한으로 발산하는 문제가 발생한다.

시간에 따른 할인 개념 도입하기

시간에 따른 할인 (Discount) 개념을 도입하며, 위에서 서술한 문제를 해결할 수 있다.

에이전트가 최대한 가까운 시점에 보상을 얻을 수 있도록 하는 것이다.

0과 1사이의 할인율을 감마 \(\gamma\)로 나타내면 다음과 같다.

상태 경로: \(s_{1} \rightarrow s_{2} \rightarrow s_{3}\)
보상 총합: \(R(s_{1})+\gamma R(s_{2})+\gamma ^2 R(s_{3})\)
상태 경로: \(s_{1} \rightarrow s_{5} \rightarrow s_{2} \rightarrow s_{3}\)
보상 총합: \(R(s_{1})+\gamma R(s_{5})+\gamma ^2 R(s_{2})+\gamma ^3 R(s_{3})\)
상태 경로: \(s_{1} \rightarrow s_{5} \rightarrow s_{1} \rightarrow s_{5} \ldots\)
보상 총합: \(R(s_{1})+\gamma R(s_{5})+\gamma ^2 R(s_{1})+\gamma ^3 R(s_{5})+\ldots\)

보상 \(R(s)\)의 값이 모두 1이라 가정하면, 보상 총합은 공비가 \(\gamma\)인 등비급수로 \(\mid \gamma \mid < 1\)이기에 수렴한다.

따라서 보상 총합이 무한으로 발산하는 문제를 해결 할 수 있다.

MDP에서 보상은 상태와 행동의 함수 \(R(s,a)\)와 마르코프 보상 과정 (MRP, Markov Reward Process)에서 사용하는 상태만의 함수인 \(R(s)\)는 다른 의미이지만, 할인율의 개념을 간단하게 보여주기 위해 사용했다.

보상 총합, 가치 함수

우리는 주어진 상태에서 최적의 행동을 찾는 방법이 필요하다.

한 에피소드에서 얻을 수 있는 보상 총합이 아닌, 주어진 상태에서 미래에 얻을 수 있는 보상 총합을 구해야한다.

이익 (Return)은 할인율과 t번째 상태를 이용해 수식으로 다음과 같이 나타낼 수 있다.

\[G_{t}=\sum \limits_{k=0}^\infty \gamma ^k R_{t+k+1}\]

이 때, 특정 상태에서 미래에 얻을 수 있는 보상의 총합, 가치함수 (Value Function)는

특정 상태에서 갈 수 있는 전체 경로에 대한 평균, 이익의 기댓값이다.

\[V(s)=E[G_{t} \mid S_{t}=s]\]

보상 (R)	특정 상태에서 얻을 수 있는 즉각적 피드백
이익 (G)	한 에피소드의 특정 상태에서 종단 상태까지 받을 수 있는 보상 총합
가치 함수 (V)	특정 상태로부터 기대할 수 있는 보상

예시로, 예방 주사를 맞을 때, 병원비와 아픔으로 즉각적인 보상은 음수. 장기적으로 건강이라는 가치를 제공하여 가치는 양수.

현재 상태의 가치 구하기, 벨만 방정식

현재 상태의 가치의 기댓값을 구하는 과정은 다음과 같다.

종단 상태를 제외한 모든 상태의 가치를 0으로 초기화한다.
- 종단 상태는 상태 전이가 없으니, 보상=가치이다.
종단 상태와 인접한 상태의 가치를 구한다.
행동의 기대 가치에 할인율을 곱한 다음 더한다.

앞서 보여준 영화 예시 그림으로 풀어 나가면 다음과 같다.

상태 \(s_{2}\)에서
행동 \(a_{2-1}\) 선택

\(s_{3}\)으로 전이할 확률: \(P(s_{3} \mid s_{2},a_{2-1})=1\)
\(s_{3}\)의 가치: \(-0\)
가치의 기댓값: \(s_{3}\)의 보상 + \(s_{3}\)의 가치 \(0\) \(\times\) 전이 확률 \(1\) \(\times\) 할인율\(0.9=-1\)

상태 \(s_{2}\)에서
행동 \(a_{2-2}\) 선택

\(s_{4}\)으로 전이할 확률: \(P(s_{4} \mid s_{2},a_{2-2})=0.6\)
\(s_{7}\)으로 전이할 확률: \(P(s_{7} \mid s_{2},a_{2-2})=0.4\)
\(s_{4}\)의 가치: \(0\)
\(s_{7}\)의 가치: \(0\)
가치의 기댓값: [전이 확률 \(0.6\) \(\times\) (\(s_{4}\)의 보상 \(-1\) + \(s_{4}\)의 가치 \(0\) \(\times\) 할인율 \(0.9\))
+ 전이 확률 0.4 \(\times\) (\(s_{7}\)의 보상 \(1\) + \(s_{7}\)의 가치 \(0\) \(\times\) 할인율 \(0.9\))]\(=-0.2\)

이 과정을 수식으로 표현하면 다음과 같은 벨만 방정식 (Bellman Equation)이 된다.

\[V(s)=max_{a} \sum \limits_{s^\prime} P(s^\prime \mid s,a)[R(s,a)+\gamma V(s^\prime)]\]

벨만 방정식은 다음 상태의 가치를 사용해서 현재 상태의 가치를 구한다.

현재를 구하기 위해 다음 상태를 계속 추적하여, 결국 종단 상태에 도달한다.

이를 코드로 구현하면 동적 계획법 (Dynamic Programming)이라는 알고리즘을 사용한다.

이처럼 동적 계획법을 기반으로 가치 함수를 산출하는 방식을 가치 반복법 (Value Iteration)이라 한다.

이제 우리는 미래 보상을 최대화하는 최적 행동을 선택 할 수 있다.

이렇게 상태를 입력으로 받아 최적 행동을 출력하는 함수를 정책 (Policy)이라 한다..

이 정책이 강화 학습에서 구하고자 하는 목표이다.

4. 정책

정책이란 지금 상태에서 해야 할 최적의 행동이 무엇인지 알려주는 것이다.

\[\pi (s)=a\]

강화 학습은 이 정책을 세워 나가는 과정이다.

가치 반복법

가치 반복법을 통해 수렴한 가치 함수는 최적의 가치 함수 (Optimal Value Function)는 \(V\pi (s)\) 이다.

이를 이용해 벨만 방정식을 조금 수정하면 다음과 같다.

\[\pi (s)=\gamma \sum \limits_{s^\prime} p(s,a) V_{\pi}(s^\prime)\]

가치 함수가 수렴 할 때까지 반복하기 보다는, 가치 갱신값 차이가 일정한 임곗값 이내에 들어오면 반복을 종료하는 방식을 사용하기도 한다.

최적의 정책 함수는 가치 함수를 업데이트 하는 가치 반복법 외에도, 정책 함수 자체를 업데이트하는 방식으로도 구할 수 있다.

정책 반복법

정책 평가 (Policy Evaluation)

정책 \(\pi (s)\)는 처음에 무작위로 초기화한다.

\(\pi (s)\)가 주어진 것은 에이전트가 어떤 상황에서 어떤 행동을 해야할지 지시받았음을 의미한다.

상태 \(s\)에서 선택할 수 있는 모든 행동에 대해 이익의 기댓값을 계산하고 최대치를 고르는 것이 아니라,

주어진 행동 \(\pi (s)\)에 대한 이익의 기댓값만 계산하면 된다.

주어진 정책에 따라 가치 함수를 구하는 일을 정책 평가 (Policy Evaluation)라 한다.

정책 개선 (Policy Improvement)

가치 함수 계산을 통해, 각 상태에서 정책 \(\pi (s)\)를 따라 행동했을 때와

정책과 아무 관련 없는 다른 행동을 선택했을 때 어느 쪽 가치가 더 큰지 알 수 있다.

정책과 무관한 다른 행동의 가치가 클 경우,

기존 정책을 가치가 더 큰 새로운 행동으로 업데이트하는 것을 정책 개선 (Policy Improvement)이라 한다.

정책 평가는 정책 함수를 기반으로 가치 함수를 갱신하고,
정책 개선은 가치 함수를 기반으로 정책 함수를 갱신한다.

정책 평가와 정책 개선을 반복하여, 가치 함수와 정책 함수가 변화하지 않는,

가치와 정책이 모두 수렴하게 하는 이것을 정책 반복법이라 한다.

\(E \rightarrow\)는 정책 평가, \(I \rightarrow\)를 정책 개선으로 하여 수식으로 표현하면 다음과 같다.

\[\pi _{0} E \rightarrow v_{\pi 0} I \rightarrow \pi _{1} E \rightarrow v_{\pi 1} I \rightarrow \ldots I \rightarrow \pi _{*} E \rightarrow v_{*}\]

정책 반복법은 가치 반복법 알고리즘보다 반복문도 깊고, 알고리즘 자체도 복잡하지만,

상황에 따라 더 빠르게 최적의 정책 함수로 수렴하기도하여, 둘 중 절대적 우위는 없다.

또한, 이들은 에이전트가 환경 안에서 가질 수 있는

모든 상태와 각 상태 간의 전이 확률을 미리 안다는 전제가 깔려 있다.

MDP를 이루는 구성 요소 중 모델에 대한 모든 지식을 미리 알고 있다는 것이다.

종단 상태로부터 역추적해 모든 상태와 행동의 가치를 계산하는 완전 탐색이라는 특징까지도,

가치 반복법과 정책 반복법은 현실 세계에 적용하기 어렵다.

참고

“Do it! 강화 학습 입문” - (이지스퍼블리싱, 조규남, 맹윤호, 임지순 지음)

깃허브: https://github.com/yunho0130/start-RL

[RL] 강화 학습 개념과 마르코프 결정, 벨만 방정식, 정책 반복법, 모델 기반 강화학습